Standing on the shoulder of giants.

Near-term quantum algorithms can benefit from the power of classical algorithms.

Zi-Jian Zhang, Thi Ha Kyaw and Alán Aspuru-Guzik

In the long run, quantum computers have huge potential for social and scientific developments. In the near-term, most quantum computing hardware's capability is still limited,  in terms of the number of qubits they possess and the number of quantum logic gates they can apply. One direct and a natural question is how to make good use of such near-term quantum computers available. It is one of the central research themes that we have been carrying out in our research group at The Matter Lab, the University of Toronto.

As we write, the study of so-called noisy intermediate-scale quantum algorithms is still in its early stages. On the one hand, classical computer algorithms are relatively mature. Why don't we leverage pre-existing classical methods to enhance quantum algorithms? We have tried to envision this concept in our recently released preprint: arXiv:2008.07553: https://arxiv.org/abs/2008.07553. We have profited from the classical renown algorithm as the density matrix renormalization group (DMRG) to accelerate quantum circuit constructions for variational quantum eigensolver (VQE) methods.

VQE: fixed circuit vs. adaptive circuit

The VQE algorithm is believed to be one of the promising quantum algorithms that can be implemented on near-term quantum computers. In VQE, a quantum circuit is built to estimate the ground state wavefunction of a given physical system-of-interest; be it a chemical molecule or a superconducting circuit, or a photonic setup. There are various approaches to VQE. Some VQE algorithms use fixed quantum circuits, in which both the number and position of quantum gates are stationary. Simultaneously, one optimizes the variational parameters, such as the angles of the rotational gates, in the circuit to approximate the objective/desired wavefunction. The fixed circuitry's rigidity usually prevents us from getting the most compact circuit for a given problem. Given that the available quantum resources limit us, an alternative pathway is to use an adaptive circuit, as shown in the figure above. The structure of the circuit can be updated iteratively. In each iteration, quantum circuits with a new structure are generated based on the previous circuit outcomes. One is then to evaluate the performance of the new ones before proceeding with another iteration. The circuit with the best performance will be selected to be the initial circuit of the succeeding iteration. Because the flexible circuits in adaptive VQE are updated in each step, they can usually achieve the same performance with much shorter quantum circuits, making them favourable for near-term quantum hardware. However, adaptive VQE methods require more time to evaluate newly generated circuits than stationary ones. One must address how to reduce the number of generated circuits, without missing out on the important ones.

Quantum mutual information

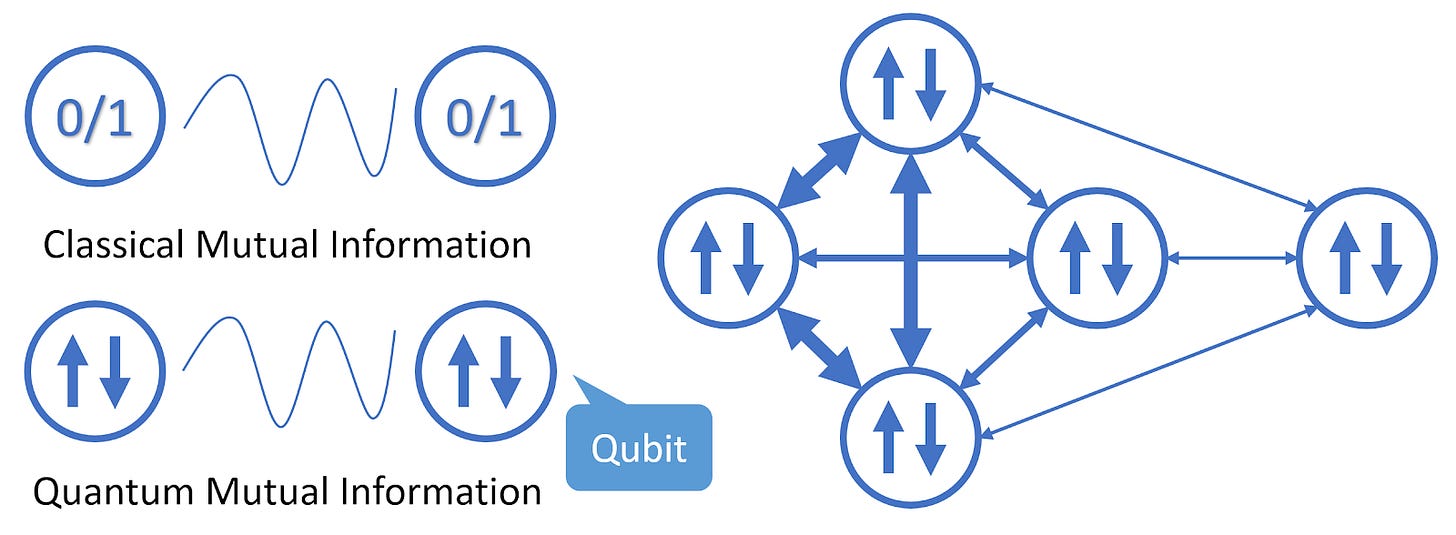
Before diving into our work details, we would like to pause here and introduce a new concept used in our work, which is quantum mutual information: an important concept in the theory of quantum information. Classical mutual information describes how much two bits are correlated. The mutual information between bits A, B quantifies how much one can learn about bit B by knowing bit A, or vice versa. When the same concept is generalized to the quantum realm, quantum mutual information quantifies how much two “qubits” are correlated, or in a fancier word: entangled. As the largest difference between the classical and quantum ones, entanglement plays a central role in quantum information science. In the above figure, we show how the quantum mutual information can vary in a system. Bolder lines mean larger mutual information and larger entanglement. With the new tool for quantifying entanglement, the objective of VQE can be understood as generating proper entanglement among the qubits giving rise to the correct ground state wavefunction, and a VQE circuit should be designed to generate such entanglement. It is natural to consider how to generate a proper VQE circuit based on the objective wavefunction's entanglement structure, or based on the quantities that reveal the structure such as the quantum mutual information. In fact, this idea has long nourished classical computational chemistry methods such as DMRG. The quantum mutual information is approximated first to guide the arrangement of the computation to achieve better performance. We want to arrange our building blocks in the same spirit, the quantum gates, according to quantum mutual information, to achieve better performance.

Adaptive circuit construction is assisted by mutual information.

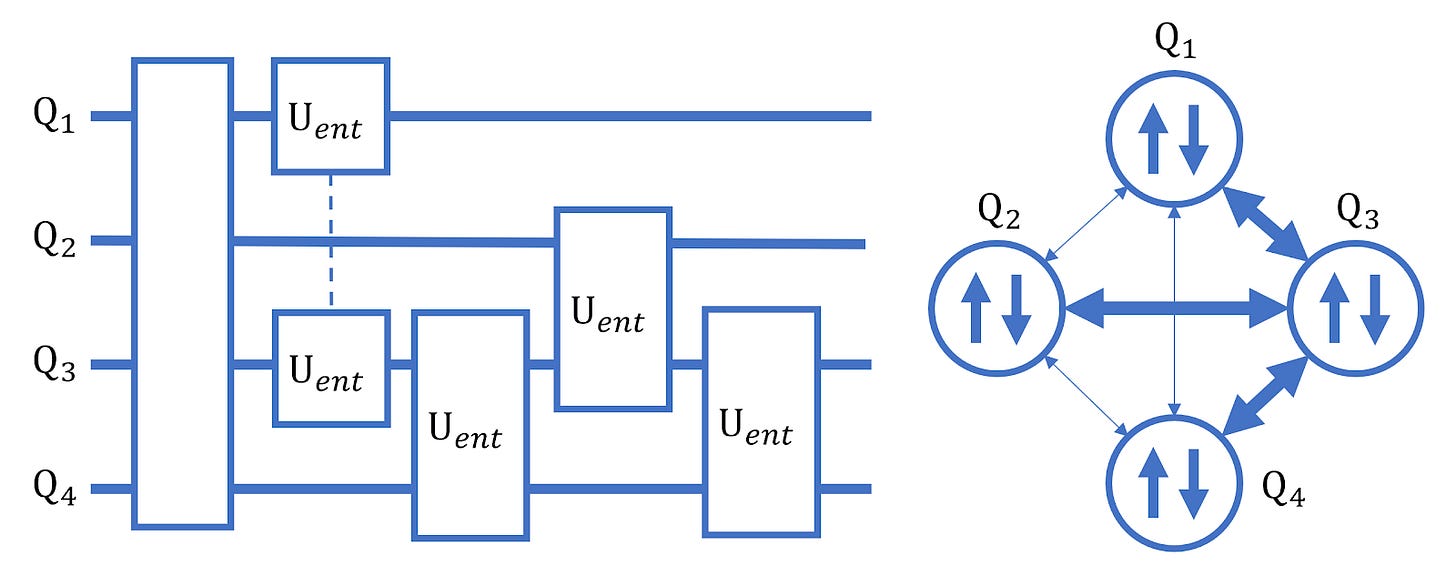
Here we introduce the steps involved in our new method. At the start, the quantum mutual information in the objective wavefunction is approximated by classical algorithms such as DMRG. In each iteration of our method, we generate new circuits in which quantum gates are mainly distributed among the qubits where the mutual information is large. By doing so, we avoid generating new circuits where quantum gates are put among the qubits that do not need to be entangled. For example, as shown in the figure, we do not try to put quantum gates between Q1 and Q2 because their quantum mutual information is small. Our numerical experiments show that we can significantly decrease the number of new circuits needed in each step of the adaptive construction by this strategy, therefore decreasing the time needed for circuit construction. Specifically, we find the number of new circuits needed to try, in some cases, can be reduced to about 5% for H2 and 10% for H2O, as compared to recently published work.

We look forward to combining this approach with many others appearing in the literature every day, making VQE research a very active endeavour in quantum computing.