Jakob Kottmann, Teresa Tamayo-Mendoza, Philipp Schleich, and Alán Aspuru-Guzik
Quantum chemistry is currently one of the most promising applications for quantum computers. However, both in quantum and classical quantum chemistry algorithms, there is a trade-off between accuracy and performance, which translates into qubit requirements. Our recent preprint demonstrates how to use a basis-set-free method from quantum chemistry to reduce the qubit numbers while keeping accuracy significantly. Here, we would like to use this space to summarize how to use this approach with an example while explaining the fundamentals of this technique. In an accompanying Jupyter notebook, we explicitly illustrate how to use Tequila to reproduce some of the results shown in this blog post and the original preprint.

One-particle space and electronic correlation
An essential part of quantum chemistry is to efficiently approximate eigenstates of electronic Hamiltonians, that describe the electronic interactions in molecules and play a crucial role in the prediction of chemical reactions. In the non-relativistic regime, this approximation can formally be divided into two major components: an accurate description of the one-particle space and electronic correlation within the many-particle wavefunction.
Quantum algorithms promise advantages to address the latter; however, even the smallest systems have relatively large qubit requirements since they rely on globally defined sets of basis functions that are not adapted to the molecular systems. Furthermore, choosing the right basis set for the correct molecular property relies on heuristics and can be challenging even for experts within the field. The basis set exchange library currently lists hundreds of Gaussian basis sets (GBS) for most atoms.
A crucial advantage of Gaussian basis sets is the fast evaluation of integrals of operators entering the electronic Hamiltonian, allowing chemists to use relatively large basis sets for their daily computations. For current quantum computers with only a very limited number of qubits available, the basis set’s size is more crucial, since the number of qubits required is directly proportional to the number of basis functions.

Our recent preprint demonstrates how to use methods from basis-set-free quantum chemistry to construct compact system-adapted qubit Hamiltonians with significantly reduced qubit numbers compared to their conventional counterparts.
This post will illustrate the fundamentals behind this technique in a minimal example: The Hydrogen molecule in two molecular orbitals (the minimum number of orbitals that allows for treatment beyond mean-field approximations). Note, however, that this system has many unique properties, and one should be careful with generalizing results from this model system. Calculations with more orbitals and with different molecules can be found in our article.
Building electronic Hamiltonians
Let’s start with the electronic Hamiltonian in second quantization. This operator represents the underlying electronic Hamiltonian in terms of second quantized operators, that create and annihilate electrons in molecular orbitals. But where do these orbitals come from?
Standard approach
In principle, they can be any set of three-dimensional orthonormal functions (as long as they fulfill certain regularity criteria, such as being square-integrable and having a bounded derivative). The predominant choice in electronic structure, however, is to use linear combinations of atomic orbitals (LCAO), where the coefficients are determined by a mean-field method like Hartree-Fock. Then, Gaussian basis-sets are used to represent the atomic orbitals. The parameters of the Gaussian basis-sets (exponents and contraction coefficients) are globally defined; usually, they are obtained by a combination of optimizations on the individual atomic systems and heuristics. Using these global basis sets, there is obviously no guarantee that they will perform as well on molecular systems as they do on atomic systems. Especially small basis sets often show poor performance.
Our approach
Basis-set-free quantum chemistry offers a way to generate TaylorMade orbitals directly for the individual molecular system. Multiresolution analysis (MRA) is one of the most advanced basis-set-free techniques for quantum chemistry. The orbitals are represented efficiently by locally increasing or decreasing the spatial resolution for each orbital individually.

Diving into the full extent of MRA lies beyond the scope of this high-level blog-post, so for now, we will just view it as a black-box way of representing and optimizing orbitals. To do so, we need to choose a surrogate model: A classically cheap model that can be solved with MRA. A first thought might be to employ the good old Hartree-Fock method simply. However, this will just result in optimized occupied orbitals (orbitals that enter the Hartree-Fock determinant), and no so-called virtual orbitals (an orthogonal set of orbitals that has no overlap with the occupied Hartree-Fock orbitals). Said virtual orbitals are an artifact of fixed basis set representations (Roothaan-Hall equations) but are not part of the actual Hartree-Fock model. Therefore, in addition to Hartree-Fock, we require a surrogate model that can produce virtual orbitals. In our work, we employed the MRA-PNO-MP2 method, which was implemented recently into madness.
This method employs the MRA machinery to directly determine optimized and localized Hartree-Fock and pair-natural orbitals on the MP2 level. After optimizing the orbitals with these surrogate models, we end up with a set of occupied Hartree-Fock orbitals and virtual pair-natural orbitals. Below, we show the radial plot of the two orbitals needed for the minimal description of the Hydrogen molecule using the STO-3G basis set.
Associated with each pair-natural orbital is an occupation number, which we can use to truncate the set to fit a given number of qubits. The integrals over these optimized orbitals can be computed with MRA techniques. They will define a compact system-adapted second-quantized Hamiltonian, which can be transformed into a qubit Hamiltonian by the usual transformations (see the Tequilanotebook).
Below, we show the radial plot of the two orbitals needed for the minimal description of the Hydrogen molecule using the STO-3G basis set and using MRA-PNOs.

Here, the minimal Gaussian basis set does a fairly good job in roughly approximating the optimized orbitals. Still, it presents limitations far from the origin and near the nuclei as well.
Including electronic correlation
From this point on, a quantum algorithm can be used to treat the second aspect of electronic structure: The accurate representation of correlations within the many-body wavefunction. We realize this with a variational quantum algorithm using the UpCCGSD model; a unitary coupled-cluster model with a generalized single electron and pair excitations between the orbitals.
The next picture shows the results for the Hydrogen molecule with different bond distances using the VQE and Hamiltonians represented with Gaussian basis sets (STO-3G) or MRA.
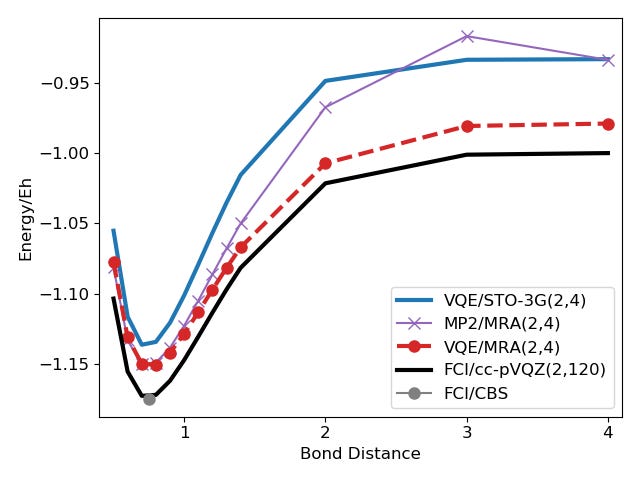
The energies of the MP2/MRA surrogate model are shown as well to emphasize that the surrogate model on its own is not powerful enough to solve the system on its own fully. This becomes clear on points with larger bond distance, where the (basis-set-free) MP2 error is as large as the basis-set error for STO-3G.
We apply the approach to a set of small molecules using different energy metrics to quantify its performance. We find significant savings in qubit requirements throughout all used accuracy metrics (see the table above).
The initial applications developed here are the first step towards improved surrogate models and higher interaction with the quantum algorithm. For instance, extended approaches could target excited states and be combined with other techniques to further reduce qubit requirements. One of them, in the form of using a special form of the Bravyi-Kitaev transformation that allows to taper-off two qubits of molecular Hamiltonians, is already illustrated in a Tequila notebook.
Stay tuned to further improvements to the variational quantum eigensolver from our group and many others that are creating several enhancements to the method.

